MAT 333 Abstract Algebra, Section 01,
CN 45122 Fall 2021
Class meets online via zoom MWF
11:30 AM - 12:45 PM, the zoom meeting information will be announced on
Blackboard
Instructor: Serban Raianu, office: NSM E-108,
office phoner: (310) 243-3139, cell phone: (657) 204-5612
e-mail address: sraianu@csudh.edu,
URL: http://math.csudh.edu/~sraianu;
office hours (same zoom link as classes): Monday,
Wednesday: 8:20 AM - 9:50 AM, Friday: 11:30 AM – 12:30 PM, or by appointment.
Course
Description: MAT 333, Abstract Algebra, covers material from
the first two chapters of the textbook: sets, groups, rings, polynomial rings,
fields.
Text: Algebra I: Groups, Rings, & Arithmetic, by Serban
Raianu, PDF available online at https://math.csudh.edu/~sraianu/algebrabook.html
Objectives: After
completing MAT 333 the student should be able to: state definitions of basic
concepts (e.g., congruence, groups, rings, integral domains, fields,
subrings, homomorphisms, ideals); understand and use the Euclidean
algorithm; understand and use modular arithmetic; state major theorems (e.g.,
the division algorithm, the unique factorization theorem, the remainder
theorem, the factor theorem, the isomorphism theorems) and be able to identify
the structures to which each theorem applies (e.g. the integers, integral
domains, polynomial rings F[x] where F is a field, groups, etc.) ; find
examples of objects that satisfy given algebraic properties (a noncommutative
ring, a commutative ring but not an integral domain, etc)
Prerequisites: MAT
271 or equivalent with a grade of "C" or better.
Grades: Grades will be based on two zoom video meetings 15-minutes
examinations (50% total), a comprehensive final examination (20%), and quizzes,
homework, video and other assignments (30%) for the remainder.
The exact grading system for your section is the following:
An oral examination will consist in giving a definition or a
statement for a notion or result studied in class, and explaining two homework
problems from the homework assignments. A list of the possible definitions and
statements is posted on Blackboard. A definition or a statement will be chosen
by selecting a random number from 1 to the number of definitions and statements
on the list. The homework problems will be selected by choosing randomly the
lecture number, then a problem number from 1 to the total number of problems in
the assignment corresponding to that lecture. For example, the
definition/statement number 5 will refer to the fifth item on the list of
possible definitions or statements on the list. The homework problem (1,13)
will refer to problem 9 in Section 1.3 in CLP-1: this is the 13th
problem in the homework assignment for Lecture 1.1. Each of the two oral exams will be graded on a 100
scale, then the sum of the scores is divided by 4 and denoted by E.
Homework will be due every week, the day
before quiz days, and each homework is worth 10 points. Each week two of the
problems from the homework due for that week will be selected and graded on a
scale from 0 to 3. The remaining 4 points will be awarded for completeness of
the homework assignment. Submitting solutions copied from the back of the book
will bring little or no credit, since copying solutions will not prepare you
for answering questions during the oral examinations. The average of all
homework scores is denoted by H. Homework will be submitted as a pdf with your
paper work on Gradescope. There is no need to match
the pages with the problems when submitting the homework, see
https://www.youtube.com/watch?v=u-pK4GzpId0
Gradescope can be accessed from the link
in Content in your Blackboard course, and you can practice submitting your work
on Gradescope using the assignment called Submission
practice, which will remain open throughout the semester. You might be asked to
explain your work on a submitted problem. Failure to provide an explanation
might result in a score of zero for the entire homework assignment. No late homework
will be accepted.
15 minutes quizzes will be given every week, and will be graded on a scale from 1 to 10. The
average of the quizzes scores is denoted by Q. While taking the quiz the video
camera on zoom needs to be on and you need to be in the frame. Each quiz will
consist of one problem, similar but not necessarily identical to one of the
homework problems assigned for that week. The quiz will be taken on Gradescope, where you will read the problem and submit your
written answers. No makeup quizzes will be offered.
There are also 10 points awarded for explaining one homework problem on video. This portion of the grade
is denoted by V. Videos will be due the day before quiz days and will have to
be uploaded on Flipgrid
https://flipgrid.com/raianu9049
The homework problems from which to choose one problem to
explain on video appear in boldface in the schedule below. No late submissions
will be accepted.
The final exam, which
will consist of fifteen problems similar to problems assigned as homework
throughout the semester, will be graded out of a maximum possible 200, then
the score is divided by 10 and denoted by F. The final exam will be taken on Gradescope, and the camera on zoom needs to be on (with you
in the frame) for the duration of the final exam. When submitting the work for
the final exam pages and problems will have to be matched, failure to do that
might result in points deducted. Webcams can be requested from the IT
department if necessary.
To determine your final
grade, compute E+H+Q+V+F. The maximum is 100, and the grade will be given
by the rule:
A: 93‑100; A‑: 90‑92;
B+: 87‑89; B: 83‑86; B‑: 80‑82
C+: 77‑79; C: 73‑76; C‑: 70‑72; D+:
67‑69; D: 60‑66; F: Less than 60. You will be able to follow your
progress in the class in Blackboard under Grade Center throughout the semester.
Accommodations
for Students with Disabilities: California State University, Dominguez Hills adheres to all
applicable federal, state, and local laws, regulations, and guidelines with
respect to providing reasonable accommodations for students with temporary and
permanent disabilities. If you have a disability that may adversely affect your
work in this class, I encourage you to register with Student disAbility Resource Center (SdRC)
and to talk with me about how I can best help you. All disclosures of
disabilities will be kept strictly confidential. Please note: no accommodation
may be made until you register with the SdRC in WH
D-180. For information call (310) 243-3660 or to use telecommunications Device
for the Deaf, call (310) 243-2028.
Academic Integrity: The mathematics department does
not tolerate cheating. Students who have questions or concerns about academic
integrity should ask their professors or the counselors in the Student
Development Office, or refer to the University Catalog for more information.
(Look in the index under "academic integrity".) Using homework
solving or derivative/integral computing websites, or collaborating in chat
rooms during tests in this class is prohibited, the penalty for being caught is
an automatic F in the class and referral for disciplinary action.
Exam and quiz rules: Students must email a picture of their CSUDH student ID at the beginning of the semester, then they have to be on zoom with the camera on for the duration of the quiz/exam. Cell phones, headphones, and browsing the internet (other than connecting to Gradescope) may not be used at all during tests.
Tentative schedule and homework assignments
M
8/23: Lecture
1.1: 1.1 Sets and functions: 1.1.2,1.1.6,1.1.7,1.1.8,1.1.11,1.1.12
(6 problems)
W
8/25: Lecture
1.2: 1.1 Sets and functions:
1.1.13,1.1.15,1.1.16,1.1.17 (4 problems)
M
8/30: Lecture
1.3: 1.2 The integers: 1.2.3,1.2.4,1.2.6,1.2.9,1.2.12 (5 problems)
W 9/1: Lecture
1.4: 1.2 The integers: 1.2.14,1.2.16,1.2.17,1.2.18,1.2.26 (5 problems)
M
9/6: Labor
Day
W 9/8: Lecture
1.5: 1.3 Equivalence relations and factor sets: 1.3.3, 1.3.5 (2 problems)
M
9/13: Lecture
1.6: 1.3 Equivalence relations and factor sets: 1.3.9,1.3.12 (2
problems)
W
9/15: Lecture
1.7: 1.3 Equivalence relations and factor sets: 1.3.19 (1
problem)
M
9/20: Lecture
1.8: 1.4 Groups and morphisms of groups: 1.4.3,1.4.4,1.4.5 (3 problems)
W
9/22: Lecture
1.9: 1.4 Groups and morphisms of groups
1.4.6,1.4.7,1.4.8,1.4.11,1.4.13
(5
problems)
M
9/27: Lecture
1.10: 1.5 Subgroups and normal subgroups:
1.5.3,1.5.4,1.5.6,1.5.8 (4 problems)
W 9/29: Lecture
1.11: 1.5 Subgroups and normal subgroups:
1.5.13,1.5.15 (2 problems)
M 10/4: Lecture
1.12: 1.6 Factor groups: 1.6.2,1.6.4 (2 problems)
W
10/6: Review
M
10/11: Oral Exam
Week 1
W
10/13: Oral Exam Week 1
M
10/18: Lecture 2.1: 1.6
Factor groups: 1.6.16,1.6.17 (2 problems)
W 10/20: Lecture
2.2: 1.7 Finite groups and the Lagrange
theorem:1.7.3,1.7.7,1.7.8,1.7.10,1.7.11 (5 problems)
M 10/25: Lecture
2.3: 1.7 Finite groups and the Lagrange theorem:
1.7.14,1.7.19,1.7.20,1.7.21 (4 problems)
W 10/27: Lecture
2.4: 2.1 Rings and morphisms of rings: 2.1.2,
2.1.4,2.1.6,2.1.7,2.1.8, 2.1.13
(6 problems)
M
11/1: Lecture
2.5: 2.2 Subrings and ideals: 2.2.2,2.2.3,2.2.5,2.2.6 (4
problems)
W 11/3: Lecture
2.6: 2.2 Subrings and ideals: 2.2.7,2.2.8,2.2.10,2.2.12 (4
problems)
M 11/8: Lecture
2.7: 2.3 Factor rings: 2.3.4,2.3.6,2.3.8,2.3.10,2.3.16 (5
problems)
W
11/10: Lecture 2.8: 2.4
Prime and maximal ideals: 2.4.2,2.4.3,2.4.5,2.4.10,2.4.12,2.4.15 (6
problems)
M 11/15: Lecture
2.9: 2.6 Polynomial rings: 2.6.3,2.6.6,2.6.7(3
problems)
W 11/17: Lecture
2.10: 2.6 Polynomial rings: 2.6.9,2.6.10 (2 problems)
M
11/22: Lecture 2.11:
2.6 Polynomial rings: 2.6.11,2.6.12 (2 problems)
W 11/24: Review
M 11/29: Oral
Exam Week 2
W
12/1: Oral
Exam Week 2
Final
examination: Wednesday, December 8, 11:30 AM - 1:30 PM.
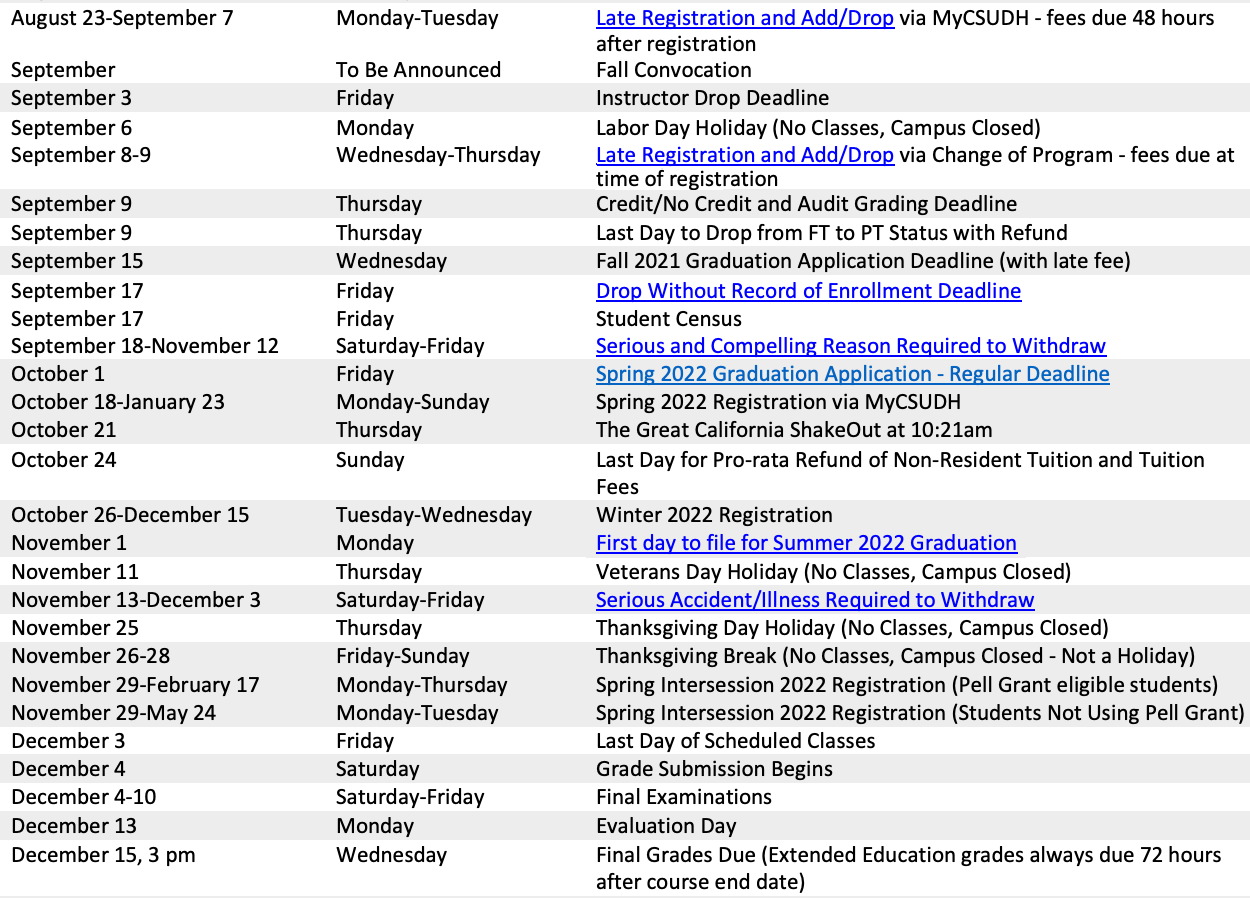
Important Dates: